Finora abbiamo considerato il calcolo di funzioni come unico modo di risolvere problemi. Oggi passiamo a studiare i problemi di appartenenza o di non appartenenza di un elemento ad un dato insieme.
Insiemi ricorsivi o decidibili
Intutitivamente, un insieme ricorsivo o decidibile è un insieme di numeri naturali per cui è possibile costruire un algoritmo che in tempo finito sia in grado di stabilire se un dato numero naturale appartiene all’insieme.
Definizione: l’insieme \(I\) è ricorsivo o decidibile se e solo se la sua funzione caratteristica
$$\chi_I(x) = \begin{cases} 1 &\text{se }x \in I \\ 0 &\text{se }x \notin I \end{cases}$$è calcolabile totale.
Esempi di insiemi ricorsivi:
- insieme vuoto \(\emptyset\)
- numeri naturali \(\mathbb{N}\)
- qualsiasi sottoinsieme finito di \(\mathbb{N}\)
- insieme complementare di un insieme ricorsivo (inverto la funzione caratteristica)
- \(\{2n \>|\> n \in \mathbb{N}\}\) , insieme dei numeri pari
- \(\{2n + 1 \>|\> n \in \mathbb{N}\}\) , insieme dei numeri dispari
- \(\{n = p + q\> |\> p, q \text{ primi}\}\) , insieme di numeri che rispettano la congettura di Goldbach
- \(I = \{(i, x, k)\>|\>\exists y, n. (x, n < k) \wedge (M_i\text{ calcola }y = \varphi_i(x) \text{ in n passi})\}\)
- \(J = \{(i, x, k, z)\>|\>\exists n. (n < k) \wedge (M_i\text{ calcola }z = \varphi_i(x)\text{ in n passi})\}\)
Per i primi sei è facile capire perché sono ricorsivi cioè basta trovare una funzione calcolabile totale che si comporta esattamente come \(\chi_I(x)\) : nel caso dei numeri pari basta che restituisca 1 se il numero è pari, 0 altrimenti; nel caso dei numeri di Goldbach basta che restituisca 1 se il numero è somma di altri 2 numeri primi, 0 altrimenti.
Gli ultimi 2 casi sono un po’ più complicati: la procedura calcolabile totale che decide I è la seguente: fai andare la MdT \(M_i\) su x < k per al massimo n − 1 passi: se nel frattempo termina poni \(\chi_I (i, x, k) = 1\) , altrimenti poni \(\chi_I (i, x, k) = 0\) . La funzione caratteristica di J è equivalente, basta anche controllare che z = y.
In questi esempi la limitazione al numero di passi è stata affidata ad una costante k, ma avremmo potuto anche usare una funzione calcolabile totale f, senza modificarne l’appartenenza agli insiemi ricorsivi.
Insiemi ricorsivamente enumerabili o semi-decidibili
Se togliamo la limitazione in passi di computazione consentiti, otteniamo un’altra classe di insiemi più ampia della precedente: quella degli insiemi ricorsivamente enumerabili o semi-decidibili.
Intuitivamente un insieme S è r.e. se esiste un algoritmo (o equivalentemente una funzione ricorsiva totale) per cui preso un certo input appartenente ad S, allora termina (o equivalentemente la funzione ricorsiva è definita).
La classe degli insiemi ricorsivamente enumerabili è un sovrainsieme stretto degli insiemi ricorsivi.
Definizione: I è ricorsivamente enumerabile o semi-decidibile se e soltanto se:
$$\exists i . I = dom(\varphi_i)$$
Un insieme ricorsivamente enumerabile è quindi il dominio di una funzione calcolabile (parziale, altrimenti \(I = \mathbb{N}\) ), che è anche detta semi-caratteristica di I.
Inoltre esiste una funzione enumeratrice f di I tale per cui \(Imm(f) = I\) . Il nome è dato dal fatto che f mette in relazione ogni elemento di I (la sua immagine) con un naturale (la sua controimmagine).
Possiamo anche formulare questa definizione usando le macchine di Turing: un insieme numerabile S si dice ricorsivamente enumerabile sse esiste una MdT tale che, se prende in input un elemento di S, allora termina.
Proprietà degli insiemi
Proprietà 1: \(I \text{ ricorsivo} \implies I \text{ ricorsivamente enumerabile}\)
Dimostrazione: sapendo che I è ricorsivo sappiamo che ha una funzione caratteristica calcolabile totale \(\chi_I(x) = \begin{cases} 1 &\text{se }x \in I \\ 0 &\text{se }x \notin I \end{cases}\) . Dobbiamo trovare \(i . I = dom(\varphi_i)\) , cioè una funzione calcolabile il cui dominio è proprio I. Possiamo definire questa:
Proprietà 2: se \(I\) è ricorsivo allora \(I, \bar I\) sono ricorsivamente enumerabili
Dimostrazione: se \(I\) è ricorsivo lo è anche il suo complementare \(\bar I\) (basta capovolgere la definizione delle funzione carattteristica di I, che resta calcolabile totale), quindi, per la proprietà 1, sia \(I\) che \(\bar I\) sono ricorsivamente enumerabili.
Proprietà 3: se \(I, \bar I\) sono ricorsivamente enumerabili allora \(I\) è ricorsivo (e lo è anche \(\bar I\) ).
Dimostrazione: devo trovare una funzione calcolabile totale che decide I, cioè devo trovare la funzione caratteristica \(\chi_I\) .
Considero \(\varphi_i, \varphi_{\bar i}\) , le funzioni i cui domini sono rispettivamente \(I, \bar I\) , per cui, dato un x, una delle due funzioni deve convergere (un elemento appartiene o non appartine ad un insieme).
La funzione calcolabile totale cercata esiste perché calcolata dal seguente algoritmo:
- Eseguo un passo di \(\varphi_i\) ;
- se \(\varphi_i \downarrow \implies x \in I \implies \chi_I(x) = 1\)
- Eseguo un passo di \(\varphi_{\bar i}\) ;
- se \(\varphi_{\bar i} \downarrow \implies x \notin I \implies \chi_I(x) = 0\)
- riparti dal punto 1
Dunque sia \(I\) che \(\bar I\) sono ricorsivi. □
Questo algoritmo è molto importante e ci consente di schivare il problema di beccare una computazione non terminante di una funzione parziale: eseguendo un passo di computazione alla volta e alternando tra una funzione e “il suo complementare” siamo sicuri che una delle due prima o poi terminerà (un elemento è in un insieme o nel complemento dell’insieme).
Teorema: se I è vuoto oppure è l’immagine di una funzione calcolabile totale allora I è ricorsivamente enumerabile.
Dimostrazione: un insieme vuoto ha come semi-caratteristica la funzione che diverge sempre e che quindi ha dominio vuoto; l’immagine di una funzione calcolabile totale ha come semi-caratteristica una funzione che converge se il suo argomento fa parte dell’immagine e diverge altrimenti. □
Teorema: se I è ricorsivamente enumerabile allora è vuoto oppure è l’immagine di una funzione calcolabile totale.
Dimostrazione: se I è ricorsivamente enumerabile allora I può essere vuoto
(e l’insieme vuoto è ricorsivamente enumerabile), oppure può essere che I è
l’immagine di una funzione calcolabile totale.
Per dimostrare questo caso costruiamo una funzione calcolabile totale f tale che
\(I = imm(f)\)
. Sappiamo per definizione di insieme ricorsivamente
enumerabile che \(I = dom(\varphi_i)\)
. Per la costruzione della funzione
f usiamo \(\varphi_i\)
e troviamo un
\(\bar n \in I \text{ tale che } \varphi_i(\bar n) \downarrow\)
.
Possiamo trovare questo \(\bar n\)
mediante un procedimento
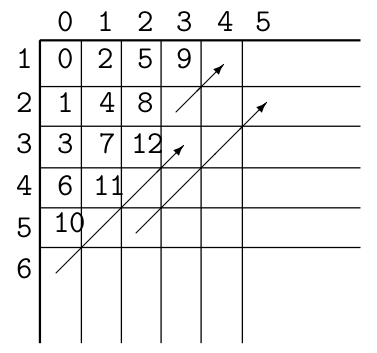
“a coda di colomba” in cui l’indice di riga m rappresenta il numero di passi del
calcolo di \(\varphi_i\)
e l’indice di colonna n il suo argomento.
Piú precisamente, si eseguono m passi nel calcolo di \(\varphi_i(n)\)
,
finché per qualche valore di m e dell’argomento \(\bar n\)
, il calcolo
si arresta. Quando ciò avviene, ovvero \(\varphi_i(\bar n) \downarrow\)
in m passi e quindi abbiamo trovato che \(\bar n \in I\)
.
Rappresentando con \(\langle n, m \rangle\)
il valore della codifica
della coppia \((n, m)\)
, iniziamo un secondo procedimento a coda di
colomba, eseguendo \(\varphi_i(n)\)
per m passi, ma, stavolta, se tale
calcolo si arresta, poniamo \(f(\langle n, m \rangle) = n\)
(perché \(n \in dom(\varphi_i) = I\)
),
altrimenti si pone \(f(\langle n, m \rangle) = \bar n\)
(per quanto
detto prima \(\bar n \in I\)
).
Si itera il procedimento incrementando la codifica
\(\langle n, m \rangle\)
, ovvero considerando
\(\langle n, m \rangle + 1\)
(in altre parole ci spostiamo in diagonale
nella tabella qui sotto) fino all’infinito.
Abbiamo costruito una funzione f che ha come immagine
\(n \in dom(\varphi_i) = I\)
e \(\bar n \in I\)
perché
\(\varphi_i(\bar n) \downarrow\)
e abbiamo generato tutti gli elementi di
I grazie al procedimento diagonale precedente (abbiamo proceduralmente applicato
\(\varphi_i\)
a tutti gli elementi del suo dominio).
□
Teorema: I è ricorsivamente enumerabile se e solamente se è vuoto oppure è l’immagine di una funzione calcolabile totale.
Dimostrazione: vedi i due teoremi precedenti. □
Insiemi speciali
Definizione:
$$K = \{x | \varphi_x(x) \downarrow\}$$
K è l’insieme degli indici delle funzioni che convergono se applicate al loro stesso indice.
Teorema: \(K\) è ricorsivamente enumerabile.
Dimostrazione: K è il dominio della funzione calcolabile parziale
che è calcolabile perché posso prendere la MdT \(M_x\) e applicarla ad x; se e quando si arresta, restituisci x.
Teorema: \(K\) non è ricorsivo.
Dimostrazione: sia \(\chi_K\) la funzione caratteristica di K e per assurdo sia totale e calcolabile. Allora anche questa funzione
Non esiste un algoritmo per decidere se \(x \in K\) e quindi abbiamo trovato un problema non decidibile, ma semi-decidibile. □
Teorema: \(\bar K\) non è ricorsivamente enumerabile (e neppure ricorsivo).
Se lo fosse varrebbe la proprietà 3 degli insiemi e \(K, \bar K\)
sarebbero ricorsivi, ma abbiamo appena dimostrato che K non è ricorsivo.
Ricordando che la classe degli insiemi r.e. sono un sovrainsieme stretto della
classe di quelli ricorsivi, allora un insieme che non è r.e. non è nemmeno
ricorsivo. Segue che \(\bar K\)
non è neppure ricorsivo.
□
Gerarchia
Ricapitolando:
- K non è ricorsivo, cioè non esiste un algoritmo per decidere se \(x \in K\) o no
- K è ricorsivamente enumerabile, cioè esiste un algoritmo che enumera le funzioni convergenti (termina se il suo input appartiene a K)
- \(\bar K\) non è ricorsivamente enumerabile (e nemmeno ricorsivo)
Abbiamo dunque scoperto che:
Più precisamente \(\bar K \in \textit{co-RE}\) , la classe dei problemi i cui complementi sono r.e., ma non ricorsivi.
Non mi è ancora del tutto chiaro se \(\textit{co-RE} \text{ e } \textit{nonRE}\) sono la stessa cosa.