Passiamo allo studio di come associare a una macchina di Turing una funzione che stimi il tempo che le è necessario per risolvere un caso x ∈ I del problema I che decide.
Già conosciamo la definzione formale di una machina di Turing deterministica e, nel caso della MdT universale, avevamo pure introdotto una macchina a 3 nastri che avevamo subito dichiarato equivalente ad una macchina ad un nastro per quanto concerne lo studio della calcolabilità. Tuttavia, come vedremo, ciò non è il caso nella teoria della complessità.
Macchina di Turing con k-nastri
Definizione: dato un numero naturale k, una macchina di Turing con k nastri è una tupla \(M = (Q, \Sigma, \delta, q_0, SI, NO)\) , con:
- \(\#,\triangleright \in \Sigma \text{ e } L, R, - \notin \Sigma\)
- \(SI, NO \notin Q\)
- \(\delta: Q \times \Sigma^k \mapsto Q \cup \{SI,NO\} \times (\Sigma \times \{L,R,-\})^k\) è la funzione di transizione, con ▷ carattere di inizio stringa
Dunque la funzione di transizione ha questa forma:
Una configurazione di una macchina a k nastri ha la forma:
Se si volesse rappresentare una situazione nella quale ci sono effettivamente k processori che evolvono in sincronia, ciascuno con il suo carattere corrente e con il suo stato preso da un insieme \(Q_i\) , basterebbe definire l’insieme della macchina a k nastri come \(Q = Q_1 \times Q_2 \times ... \times Q_k\) e interpretare la funzione di transizione opportunamente in modo da tenerne conto.
Ad esempio una macchina di Turing a 2 nastri che controlla se una stringa è palindroma, può operare nel seguente modo:
- copia la stringa dal primo al secondo nastro, facendo scorrere le due testine in sincrono, la prima legge e la seconda scrive
- fai arretrare la prima testina ad inizio stringa e lascia la seconda alla fine
- inizia a cancellare i caratteri dal secondo nastro a partire dal fondo se e soltanto se corrispondono a quelli che si trovano sul primo.
- la macchina termina nello stato NO se vengono incontrati caratteri che non combaciano
- la macchina termina nello stato SI se il secondo nastro è vuoto.
Ecco una possibile MdT a 2 nastri che risolve il problema della stringa palindroma sull’alfabeto {a, b}:
| q σ1 σ2 | δ(q, σ1 , σ2) |
|---|---|
| q0 ▷ ▷ | q0 (▷, R) (▷, R) |
| q0 a # | q0 (a, R) (a, R) |
| q0 b # | q0 (b, R) (b, R) |
| q0 # # q1 | q1 (#, L) (#, −) |
| q1 a # q1 | q1 (a, L) (#, −) |
| q1 b # q1 | q1 (b, L) (#, −) |
| q1 ▷ # q2 | q1 (▷, R) (#, L) |
| q2 a a q2 | q1 (a, R) (#, L) |
| q2 b b q2 | q1 (b, R) (#, L) |
| q2 a b NO | q1 (a, R) (a, −) |
| q2 b a NO | q1 (b, R) (b, −) |
| q2 # ▷ SI | q1 (#, −) (▷, R) |
Come esempio di calcolo applichiamo la macchina alla stringa abba, raggruppando i passi della computazione in blocchi omogenei:
- Copia della stringa:
$$(q_0, \underline{\triangleright} abba, \underline{\triangleright} \#) → (q_0, \triangleright \underline{a}bba, \triangleright \underline{\#}) → (q_0, \triangleright a \underline{b}ba, \triangleright a \underline{\#}) →^3 (q_0, \triangleright abba\underline{\#}, \triangleright abba \underline{\#}) → $$
- Sposta testina 1 all’inizio del nastro:
$$(q_1, \triangleright abba \underline{\#}, \triangleright abba \underline{\#}) → (q_1, \triangleright abb \underline{a} \#, \triangleright abba \underline{\#}) →^4 (q_1, \underline{\triangleright} abba, \triangleright abba \underline{\#}) →$$
- Cancella carattere per carattere dal nastro 2:
$$(q2 , \triangleright \underline{a}bba, \triangleright abb\underline{a} \#) → (q_2, \triangleright a\underline{b}ba, \triangleright ab\underline{b} \#) → (q_2, \triangleright ab\underline{b}a, \triangleright a\underline{b} \#) → \\ (q_2, \triangleright abb\underline{a}, \triangleright \underline{a} \#) → (q_2, \triangleright abba \underline{\#}, \underline{\triangleright}) → (SI, \triangleright abba \underline{\#}, \triangleright \underline{\#}).$$
La macchina ha accettato la stringa abba che infatti è palindroma.
Complessità in tempo deterministico
Definizione: diciamo che t è il tempo richiesto da una MdT a k nastri per decidere il caso \(x \in I\) se
Tuttavia, come abbiamo già detto, vogliamo trovare una funzione che approssimi e limiti il tempo necessario al calcolo in base alla taglia |x| dell’input della macchina M. Nella maggior parte dei casi misureremo la taglia in relazione alle caselle della MdT necessarie a contenere il dato di input.
Definizione: M decide I in tempo deterministico f se per ogni dato di ingresso x il tempo t richiesto da M per decidere x è minore di o è uguale a \(f(|x|)\) .
Classe di complessità in tempo deterministico
Definizione:
$$\mathrm{TIME}(f) = \{I | \exists M \text{ che decide I in tempo deterministico } f\}$$
La classe di complessità appena introdotta contiene tutti e soli i problemi risolvibili in tempo deterministico f, ovvero affinchè un problema vi appartenga occorre e basta che esista una macchina M che lo decide in tempo deterministico f.
Calcoliamo la complessità dell’esempio precedente sulle stringhe palindrome:
- copia della stringa n + 1 passi
- ritorna all’inizio n + 1 passi
- sposta le due testine se i simboli sono uguali n + 1 passi
Il totale è 3n + 3 passi + 1 passo per l’accettazione. Il problema appartiene a TIME(3n + 4). Però le costanti non ci interessano, ci basta dire che è 3n + 4 è dell’ordine di n.
Più avanti faremo uso della notazione O-grande, dandola per già nota. Sul web ci sono ottime risorse come queste: 1, 2 e 3.
Scriveremo robe come \(\mathcal{O}(n), \mathcal{O}(log(n)), \mathcal{O}(2^n)\) , riesumando alcune tra le più occulte nozioni di analisi matematica:
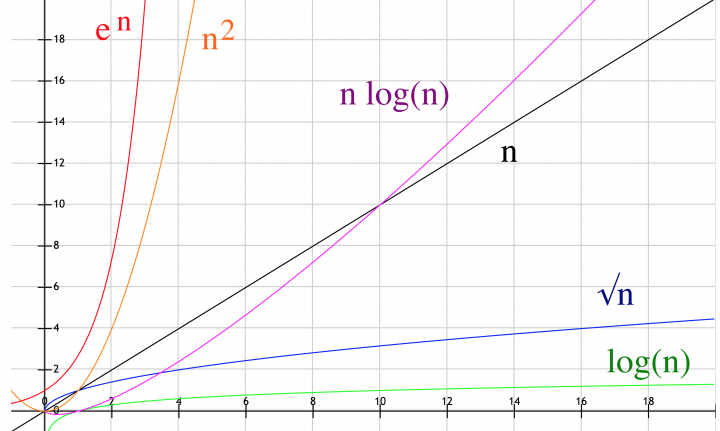
Teorema di riduzione del numero di nastri
Teorema: data una macchina di Turing M con k nastri che decide I in tempo deterministico > f, allora \(\exists M'\) con 1 nastro che decide I in tempo deterministico \(\mathcal{O}(f^2)\) .
Dimostrazione: costruiamo M’ in modo che simuli M in modo analogo a quanto fatto nella costruzione della macchina di Turing Universale.
Ogni configurazione di M nella forma
viene simulata da:
cioè racchiudiamo ciascun nastro \(w_i σ_i u_i\) tra due nuove parentesi 【 e 】 e usiamo #Σ nuovi simboli \(\overline{\sigma_i}\) per ricordarci di qual era la posizione della testina sull’i-esimo nastro.
Per cominciare, la macchina M’ applicata a x dovrà generare la configurazione che simula la configurazione iniziale di M, cioè dobbiamo passare dalla configurazione iniziale di \(M, (q_0, \triangleright x, \triangleright, ..., \triangleright)\) a \((q, \triangleright 【 x 】 (【】)^{k−1})\) , per qualche q.
Per far ciò, bastano 2k + #Σ nuovi stati e un certo numero di passi che, essendo dell’ordine di |x|, non influenza la complessità asintotica (consideriamo infatti il caso pessimo, quindi tutto il dato iniziale va letto).
Per simulare una mossa di M, la macchina M’ scorre il dato di ingresso da sinistra a destra e viceversa due volte:
- la prima volta M’ determina quali sono i simboli correnti di M, \(\overline{\sigma_1}\) (si noti che, per ricordare quale sia la stringa \(\overline{\sigma_1} ... \overline{\sigma_k}\) sono sufficienti \((\# \Sigma)^k\) nuovi stati).
- la seconda volta M’ scrive i nuovi simboli nel posto giusto — attenzione! se un 】 deve essere spostato a destra per far posto a un nuovo simbolo da scrivere, si verifica una cascata di spostamenti a destra!
Infine, quando M si ferma, anche M’ si ferma, eventualmente rimuovendo tutte le parentesi 【 e 】 e sostituendo i caratteri \(\overline{\sigma_i}\) con \(\sigma_i\) .
Una macchina non può toccare un numero di caselle maggiore del numero dei passi che compie. Di conseguenza, la lunghezza totale del nastro scritto è al piú \(K = k \times (f (|x|) + 2) + 1\) (l’addendo 2 è dovuto alle parentesi 【 e 】, l’addendo 1 al simbolo ▷).
Allora, andare due volte avanti e indietro costa, in termini di tempo, per ogni stringa simulata 4K (più al massimo 3K per gli spostamenti a destra, nel caso in cui la casella corrente sia all’estrema sinistra: K per arrivare alla fine del nastro scritto e 2K per spostare a destra i K caratteri).
Possiamo concludere che per simulare un singolo passo di M la macchina M' richiede \(\mathcal{O}(f (|x|)\) passi sul dato x. Il numero dei passi di M’ sull’intera computazione è quindi in \(\mathcal{O}(f (|x|)^2)\) , perchè M richiede tempo f(|x|) e perché M' impiega \(\mathcal{O}(f (|x|))\) per simulare ogni passo di M.
Infine, per costruzione M’ è equivalente a M e quindi le due macchine decidono lo stesso problema; allora M’, che ha un nastro solo, decide tale problema in tempo deterministico \(\mathcal{O}(f (|x|)^2)\) . □
La conseguenza di questo teorema è che l’aggiunta di nastri ad una macchina di Turing non ne modifica il tipo di funzioni calcolabili e non modifica il tempo deterministico richiesto se non polinomialmente.
Osservazione: il tempo limita lo spazio
Notiamo che se una MdT richiede tempo \(f(|x|)\) per decidere \(x \in I\) , significa che si arresta in un numero di passi inferiore a \(f(|x|)\) e quindi non può aver visitato in alcuno dei suoi nastri un numero di caselle superiore a \(f(|x|)\) . Di conseguenza abbiamo trovato che non è possibile che una MdT richieda più spazio che tempo!
Corollario
Le macchine parallele sono polinomialmente piú veloci di quelle sequenziali.
Teorema di accelerazione lineare MdT
Il teorema di accelerazione lineare per le macchine di Turing dimostra che lo spazio e il tempo richiesti da una macchina di Turing per risolvere un problema decidibile possono essere ridotti, di un qualunque fattore costante moltiplicativo. Come conseguenza si ha che è sempre possibile migliorare la velocità di esecuzione di un algoritmo (a patto di utilizzare più memoria) oppure che è sempre possibile diminuire lo spazio occupato in memoria (a patto di aumentare il tempo di esecuzione), tuttavia i miglioramenti sono al più lineari.
Un altro esempio potrebbe essere quello della possibilità di far girare programmi compilati a 32 bit su processori a 64 bit: lo stesso programma compilato con istruzioni a 64 bit può essere più rapido di un fattore lineare dello stesso programma compilato a 32 bit.
Teorema: Se \(I \in \mathrm{TIME}(f)\) , allora \(\forall \epsilon \in \mathbb{R}^+\) si ha che \(I \in \mathrm{TIME}(\epsilon \times f(|x|) + |x| + 2)\) .
Dimostrazione (schematica): (può essere utile vedere wikipedia) costruisci M’ a partire da M (macchine con n nastri) che risolve il problema I, seguendo queste linee guida:
- compattare m simboli di M in 1 simbolo di M’, espandendo l’alfabeto di M’ con i simboli \(\Sigma^m\) , quindi \(\Sigma' = \Sigma \cup \Sigma^m \) .
- gli stati di M’ saranno triplette \((q, \sigma'_i, k)\) che codificano la configurazione di M: M si trova nello stato q, e ha il cursore sul k-esimo simbolo \(\sigma'_i = \sigma_{i1},...,\sigma_{im}\) . Ad esempio il nastro di M [▹ _ a b b a b b a _ …] viene codificato da M’ come [▹ (_,a,b) (b,a,b) (b,a,_) …].
- l’operazione di codifica del dato in input ad M richiede n + 2 passi, con \(n = |x| \leq m \times \lceil {|x| \over m} \rceil + 2 \)
- M’ necessita di 6 passi per simulare m passi di M:
- 4 passi per codificare in M’ i simboli a sinistra e a destra della testina:
- destra, codifica simbolo a destra della testina
- sinistra
- sinistra, codifica simbolo a sinistra della testina
- destra, ritorna in posizione di partenza
- 2 passi per aggiornare lo stato di M’ simulando m transizioni di M:
- aggiorna il simbolo corrente (eventualmente)
- aggiorna il simbolo adiacente (eventualmente)
- 4 passi per codificare in M’ i simboli a sinistra e a destra della testina:
- la simulazione di M richiede in totale \(6 \times \lceil {f(|x|) \over m} \rceil + |x| + 2\) passi.
- ricordando che \(I \in \mathrm{TIME}(\epsilon \times f(|x|) + |x| + 2)\) se poniamo che \(m = \lceil {6 \over \epsilon} \rceil\) , otteniamo che M' simula M in al più \(6 \times \lceil {f(|x|) \over m} \rceil + |x| + 2\) passi, quindi \(I \in \mathrm{TIME}(\epsilon \times f(|x|) + |x| + 2)\) . □
Definizione: la classe dei problemi decidibili in tempo polinomiale su una macchina di Turing deterministica a singolo nastro è
$$\mathcal{P} = \bigcup_{k \geq 1} \mathrm{TIME}(n^k)$$
La centralità di questa classe nello studio della teoria della complessità è giustificata da questi motivi:
- P è invariante per tutti i modelli di calcolo che sono polinomialmente equivalenti ad una MdT deterministica a nastro singolo.
- P corrisponde approssimativamente alla classe dei problemi che sono realisticamente risolvibili su un computer.